Engineers in the field always say that a lot of what students learn in college will not be used in their work. All those head-cracking formulas, constants and problem solving will be thrown out of the window once engineering students reach their graduation day, they suggest. But that should not always be the case.
If you are a civil engineering student, you’ll see in your curriculum a subject called Fluid Mechanics. Some engineering fields like chemical and mechanical may offer this subject as required, but fluid mechanics is necessary for civil engineering students who might work with dams, sewers, channels and any water containment.
Having to learn the subject myself, believe me when I say that there are only three essential things that you need to hold on in your Fluid Mechanics class, and these are the following:
The Continuity Equation
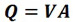
Where:
Q = flow (cfs)
V = velocity (ft/s)
A = cross-sectional area of flow (sq. ft)
This equation is used in designing and analyzing storm sewers and open channels, considering the mass conservation for a steady, one-dimensional flow, with one inlet and one outlet. This formula assumes that the fluid is incompressible or that the density of the fluid is constant.
The Energy Equation
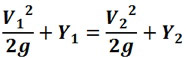
Where:
Y = elevation head or potential energy
V2/2g = kinetic energy
All orifice and weir equations are derived from the energy equation. We learn from basic physics that the energy, E1 at point 1 always equals the energy at point 2, E2. That energy is composed of two, which is the potential energy and kinetic energy, always constant at any point.
Manning’s Equation
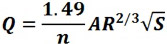
Where:
Q = discharge
n = roughness coefficient
A = channel cross-sectional area
R = hydraulic radius = area / wetted perimeter
S = slope of energy grade line
This formula by Robert Manning might have scared civil engineering students at first look, but it’s quite the most commonly used discharge equation that applies to uniform flow in open channels and is a function of the channel velocity, flow area and channel slope.
