An engineering student is always bombarded with numerical and worded problems that need step-by-step solutions to arrive to the answers. Solving these problems enable learning of the subject matter at hand with an aim to apply the principles in real life. After all, that’s what engineering is for.
But how does one approach a problem correctly? Just follow these three basic steps:
State the given.
Particularly for worded problems, the first critical step in solving any engineering problem is to gather the given information and known quantities.
There will be cases that your professor will feed you with values you don’t need to confuse or test your ability to separate what is needed in the problem. But sometimes, there are values that are not provided like the value of g or pi which are also essential. It has to be made sure as well that all the values belong to the same system of units, like in measurements feet versus meter, kilogram versus pound, so convert the values right away as necessary to avoid confusion later.
Moreover, do not forget the so-called boundary conditions, or constraints that apply to the problem.
Find the required.
The problem usually states explicitly what it is looking for, so focus on that. It is recommended to assign a symbol for the unknown.
Write it so you would not forget including the unit. It’s just like setting a goal that you need to arrive to.
Show the solution.
It sounds simple, but a solution is more than just a computation – it needs to have first a free body diagram (FBD), or a sketch complete with labels to be able to visualize the variables in aid of interpreting the problem.
Even if it is not needed, as the one who solves the problem it might give you a better understanding of the given values. Name and label the parts of the sketch accordingly.
Based on the FBD, the next questions you need to ask yourself are the following, not necessarily in particular order:
- What principles or formulas are to be applied in this problem?
- What could be the underlying assumptions or conditions?
- Is there only one way to interpret the problem or one way to solve it?
- Can the sketch be simplified further?
Once everything has been settled and simplified, do the math algebraically then numerically with the calculator. It pays to be careful to press the right buttons, so at this point there is no reason to make a mistake if you are doing the correct math.
You can perform several computations with your mind having the confidence with your arithmetic, but then this could be prone to human error. Each level of the equation should be written to avoid this and even the most basic 3×3 is to be done in a calculator to make sure it is the correct answer 9.
To complete the solution, box the final answer for it to be identified right away, which should be in line with the “required” item previously defined. In some cases, it might need to be presented in graph or tables.
But before submission, double check each step of the solution. Always.
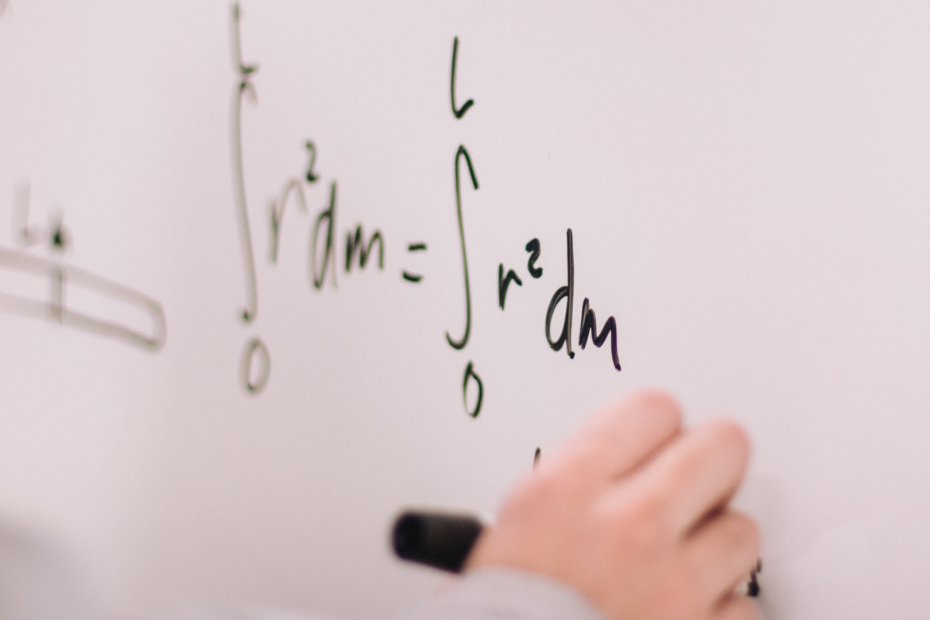
Thanks