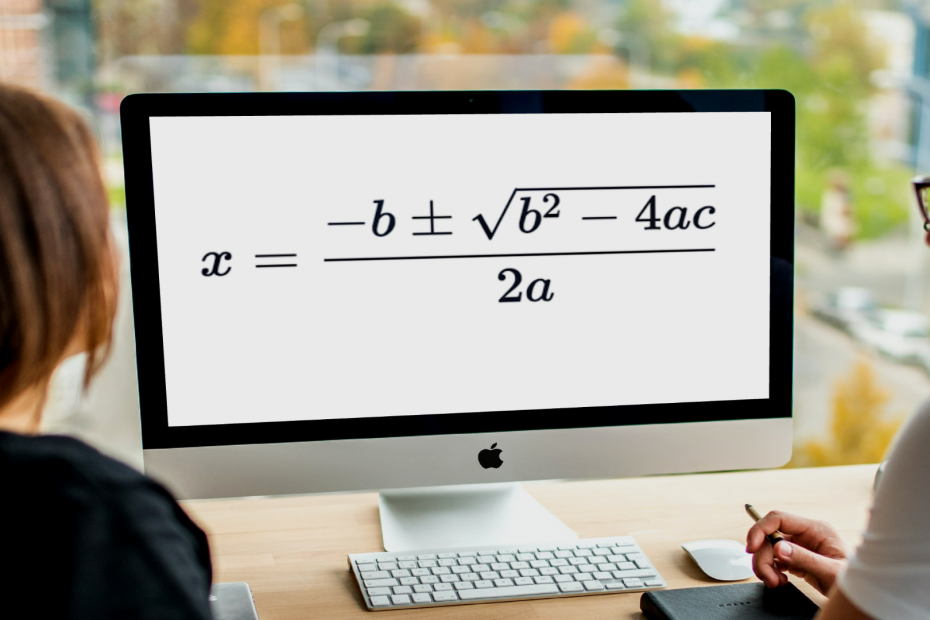Just looking at the quadratic equation makes your head hurt, mostly because it can be quite complicated to memorize and use as a solution for quadratic equations. Arguably, it is still a reliable method.
Of course, there is also factoring and completing the squares, but Professor Po-Shen Loh, a mathematician from Carnegie Mellon University, discovered in 2019 another way to solve quadratic equations that might be the simplest of them all.

He describes it as a “computationally-efficient, natural, and easy-to-remember algorithm for solving general quadratic equations”.
So how does it work? You may watch this video below, or read the explanation that follows:
In reference to factoring the quadratic x² + bx + c, Loh explains that instead of looking for the product of two numbers that make up c, we could look for two numbers to put in the blanks with sum -b and product c. His technique uses averaging that focus on the sum.
“The sum of two numbers is 2 when their average is 1,” he says.
“So, we can try to look for numbers that are 1 plus some amount, and 1 minus the same amount. All we need to do is to find if there exists a u such that 1 + u and 1 − u work as the two numbers, and u is allowed to be 0.”
To understand this better, you may go to this Loh’s website for examples.
No prior evidence can be found about this method, and the only closes one is an 1989 research article but was a similar work.
What do you think about this quadratic solution?